Sau bài này em sẽ:
- Biết hệ nhị phân là gì và cách biểu diễn số nguyên trong máy tính.
- Hiểu cách đổi giữa hệ thập phân và nhị phân.
- Thực hiện được các phép cộng, nhân trong hệ nhị phân.
- Giải thích được vì sao máy tính lại “chỉ biết 0 và 1”.
1. HỆ NHỊ PHÂN VÀ BIỂU DIỄN SỐ NGUYÊN
a) Hệ nhị phân
Con người chúng ta quen dùng hệ thập phân (cơ số 10), gồm các chữ số 0–9.
Nhưng máy tính thì “đơn giản” hơn – nó chỉ hiểu hai trạng thái: có điện (1) và không điện (0).
Đó chính là hệ nhị phân (cơ số 2).
Mỗi số trong hệ nhị phân được viết bằng các chữ số 0 và 1, trong đó mỗi vị trí có giá trị gấp đôi vị trí bên phải.
Ví dụ:
- Trong hệ 10: 513 = 5×10² + 1×10¹ + 3×10⁰
- Trong hệ 2: 19₁₀ = 1×2⁴ + 0×2³ + 0×2² + 1×2¹ + 1×2⁰ = 10011₂
💡 Ghi nhớ: Hệ nhị phân = chỉ có 0 và 1, mỗi bit (binary digit) là một “chữ số” trong hệ này.
b) Đổi biểu diễn số nguyên dương từ hệ thập phân sang hệ nhị phân
Để đổi một số từ hệ thập phân (10) sang hệ nhị phân (2), ta chia liên tiếp cho 2, ghi lại phần dư, rồi đọc các số dư từ dưới lên.
Ví dụ:
19 ÷ 2 = 9 dư 1
9 ÷ 2 = 4 dư 1
4 ÷ 2 = 2 dư 0
2 ÷ 2 = 1 dư 0
1 ÷ 2 = 0 dư 1
→ 19₁₀ = 10011₂
Ngược lại, để đổi từ nhị phân sang thập phân, ta tính tổng các luỹ thừa của 2 tương ứng với các chữ số 1.
Ví dụ:
1101₂ = 1×8 + 1×4 + 0×2 + 1×1 = 13₁₀.
💬 Mẹo nhỏ: “Chia 2 – ghi dư – đọc ngược”, nhớ câu này là khỏi lo lẫn!
c) Biểu diễn số nguyên trong máy tính
Máy tính lưu trữ số bằng bit (0, 1). Tùy độ lớn của số, nó dùng 1 byte (8 bit), 2 byte (16 bit)…
- Số nguyên không dấu: chỉ biểu diễn giá trị dương, giống việc đổi số từ hệ thập phân sang hệ nhị phân, ví dụ:
19₁₀ = 00010011₂. - Số nguyên có dấu: dùng 1 bit đầu tiên làm bit dấu:
- 0 = số dương,
- 1 = số âm.
Có nhiều cách mã hoá số âm, phổ biến là:
- Mã thuận (dấu–lượng)
- Mã bù 1 (đảo bit)
- Mã bù 2 (mã được dùng nhiều nhất trong máy tính)
Ví dụ:
- +19 → 00010011
- –19 →
- Mã thuận: 10010011
- Mã bù 1: 11101100
- Mã bù 2: 11101101
Câu hỏi & hướng dẫn trả lời:
Câu hỏi & Hướng dẫn
- Em hãy đổi 13₁₀ sang hệ nhị phân.
→ Chia 2 liên tiếp: kết quả 1101₂. - Em hãy đổi 110011₂ sang hệ thập phân.
→ 1×2⁵ + 1×2⁴ + 0×2³ + 0×2² + 1×2¹ + 1×2⁰ = 51₁₀.
2. CÁC PHÉP TÍNH SỐ HỌC TRONG HỆ NHỊ PHÂN
Máy tính chỉ biết 0 và 1, nên các phép cộng, trừ, nhân… đều được thực hiện trên hệ nhị phân.
a) Bảng cộng và nhân trong hệ nhị phân
Bảng cộng và nhân trong hệ nhị phân tương tự hệ thập phân.
⚡ Lưu ý: “1 + 1 = 10” – nghĩa là 2 trong hệ 10 nhé, đừng nhầm là mười nha 😄
b) Cộng hai số nhị phân
Giống như cộng số thập phân, nhưng chỉ có hai chữ số 0 và 1.
Quy tắc:
- 0 + 0 = 0
- 0 + 1 = 1
- 1 + 0 = 1
- 1 + 1 = 10 (ghi 0, nhớ 1 sang trái)
Ví dụ:
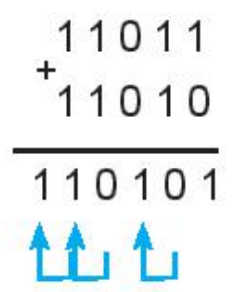
c) Nhân hai số nhị phân
Tương tự phép nhân thông thường: nhân từng chữ số, rồi cộng các kết quả theo hàng.
Ví dụ:
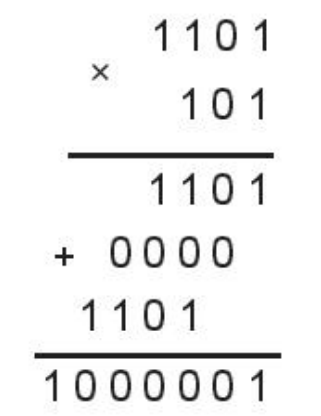
LUYỆN TẬP
Quy trình tính toán trong máy tính
Khi em gõ 125 + 17, máy tính thực hiện:
- Mã hoá sang hệ nhị phân.
- Tính toán trong hệ nhị phân.
- Giải mã ngược lại để hiển thị kết quả ở hệ 10.
Đó chính là chu trình:
Mã hoá → Tính toán → Giải mã
Câu hỏi & hướng dẫn trả lời
Câu hỏi & Hướng dẫn
- Thực hiện 101101 + 11001 trong hệ nhị phân.
→ Kết quả: 1000110₂ = 70₁₀. - Thực hiện 100111 × 1011 trong hệ nhị phân.
→ Kết quả: 110010101₂ = 405₁₀.
Luyện tập
- 125 + 17 = ?
→ 125₁₀ = 1111101₂, 17₁₀ = 10001₂ → cộng → 1111101 + 10001 = 10011110₂ = 142₁₀. - 15 × 6 = ?
→ 15₁₀ = 1111₂, 6₁₀ = 110₂ → nhân → 101010₂ = 90₁₀. - 250 + 175 = ?
→ 250₁₀ = 11111010₂, 175₁₀ = 10101111₂ → cộng → 110101001₂ = 425₁₀.
VẬN DỤNG
- Tìm hiểu cách đổi phần thập phân sang nhị phân.
→ Nhân phần thập phân với 2, lấy phần nguyên, tiếp tục với phần lẻ… đến khi hết hoặc lặp lại. - Tìm hiểu mã bù 2.
- Đảo tất cả các bit của số (0 → 1, 1 → 0), sau đó cộng thêm 1.
- Dùng để biểu diễn số âm, giúp máy tính cộng trừ nhanh và chính xác hơn.
Tóm lại
- Hệ nhị phân là “ngôn ngữ mẹ đẻ” của máy tính.
- Mọi dữ liệu (số, chữ, hình, âm thanh…) cuối cùng đều được chuyển thành chuỗi 0 và 1.
- Hiểu được hệ nhị phân là bước đầu để “nói chuyện” với máy tính – và tin vui là: nó rất dễ thương, chỉ biết “có” hoặc “không”! 😄
Views: 1


